Introduction

Structures with periodicity in three dimensions can be constructed so that they posses an omnidirectional photonic bandap. Light with frequencies lying within this band gap cannot propagate regardless of polarization and incidence angle. By locally altering the crystal properties, one may engineer a "defect" in such a way to allow a defect mode to exist within the band gap. Since the defect is surrounded by the periodic material possessing an omnidirectional bandgap, the light is confined to the defect region.

If one creates a linear defect region, it can propagate light like a wave guide. Unlike conventional wave guides, a photonic crystal wave guide can be constructed to allow sharp bends without loss. Similarly, a point defect will act as a resonator. Add some active material and you can create micro-sized amplifiers and lasers. If you add variable index material to branching waveguides, you can create a switch. 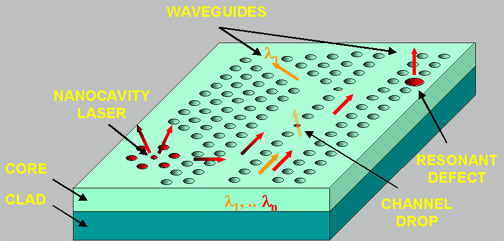Combining resonators and wave guides, you create add/drop multiplexers, and so on. All sorts of optical circuit devices have been proposed. Below is an artist's rendition of such a optical chip. The drawing is a conceptual illustration only, and not to any sort of scale.

Modeling and Simulation

Frequency Domain Calculations - The first step in modeling a photonic crystal is to produce a dispersion diagram of the crystal with no defects present. This determines if a band gap exists, and if so, its size and location in frequency. Once that information is determined, a dispersion diagram of the defect is constructed.

Time Domain Calculations - In order to find the transmission properties of the photonic crystal with its defect structure, one uses finite-difference time domain calculations. With FDTD, one can find the transmission properties of a photonic crystal waveguide, including transmission around sharp bends. FDTD can also account for material losses. But most importantly, the transmission results can be compared directly to experimental results.

Parallel Computing with FDTD - I begin most calculations in 2D (periodicity in the x & y directions with z assumed to be uniform). This gives a rough estimate of the photonic crystal properties with minimal computational requirements. However, modeling the full 3D problem with FDTD requires enormous computational resources. Fortunately, FDTD is well suited to parallel computing techniques.

Miscellaneous